The energy stored in a capacitor with capacitance
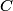 is is 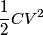 where 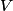 is the voltage difference between the two plates. The effect of adding a dielectric with dielectric constant is the voltage difference between the two plates. The effect of adding a dielectric with dielectric constant 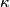 is to multiply the capacitance by is to multiply the capacitance by 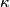 . So, given that the voltage is fixed, the stored energy is increased by a factor of . So, given that the voltage is fixed, the stored energy is increased by a factor of 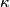 , becoming , becoming 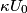 . The electric field between the plates is . The electric field between the plates is 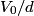 regardless of whether there is a dielectric between the plates or not. Therefore, answer (B) is correct. regardless of whether there is a dielectric between the plates or not. Therefore, answer (B) is correct. |